Biological materials such as tissues and actomyosin networks display properties of active nematic (or, more generally, ordered) fluids. The individual constituents of these systems convert chemical energy into mechanical work, enabling them to flow on long time scales. These self-driven flows play a crucial role in biological processes like morphogenesis and tissue organization. Since such flows often occurs in thin biological structures, such as the cellular cortex or epithelial tissues, this motivates the theoretical concept of an active surface. In this thesis, we explore the physics of such rigid active surfaces through mainly two types of projects: purely theoretical exploration, and modeling projects developed in collaboration with experimentalists.
For theoretically exploration, our starting point is active gel theory: a fully covariant theory of the hydrodynamics of nematic and polar active surfaces. This continuum theory describes the long-timescale behavior of such systems, assuming constant consumption of chemical fuel. Firstly, we re-examine the classic active matter problem of stability +1 defect, now extended to axi-symmetric curved surfaces. We find that for an active film on a curved, rigid frictionless substrate, a generic nematic (Frank) elastic energy coupling to extrinsic curvature can result in localized active flows to regions where the difference in principal curvatures is smallest. This leads to interesting differences with respect to flat space active instabilities including threshold-less active flows, hysteresis and bistability. These findings illustrate how tissue geometry (i.e., curvature) can aid in constraining active nematic flows.
We also found that this same coupling to curvature can trigger front propagation in the nematic alignment field. The phenomenon isn’t specific to any surface, and also holds on flat surfaces and also in defect-free configurations. The front solutions observed exhibit distinct regimes: classic FKPP-like ('pulled') fronts, where a stable nematic order invades an unstable order, and 'pushed' fronts, where a stable order invades a metastable order. We have also found an exact expression for the front speed and front profile in the pushed case, and the value of flow alignment at the transition from pushed to pulled. These results could be relevant to active nematic turbulence, and also show a possible mechanistic way of transmitting orientation cues.
In the first modeling work I present, I consider a curved active surface whose individual constituents—in addition to possessing nematic order and activity—also exhibit broken chiral symmetry. Our experimental collaborators observed that on cylindrical surfaces, elongated Myoblats cells self-organize into helical superstructures with robust right-handed chirality. To understand this phenomenon of how a robust chirality emerges on a tissue level, we develop a theoretical model by identifying two key chiral contributions: an energetic term favoring right-handed twisted helical order formation, and an active torque term arising from substrate coupling. We validated our model by testing it against experimental observations on increasingly complex substrates, thereby demonstrating how intrinsic chirality propagates across scales - from individual cells to collective tissue-level organization.
The majority of the thesis focuses on the physics of rigid active surfaces. But, in real biological systems, these active surfaces are usually deformable and are also capable of exerting forces on their surroundings.
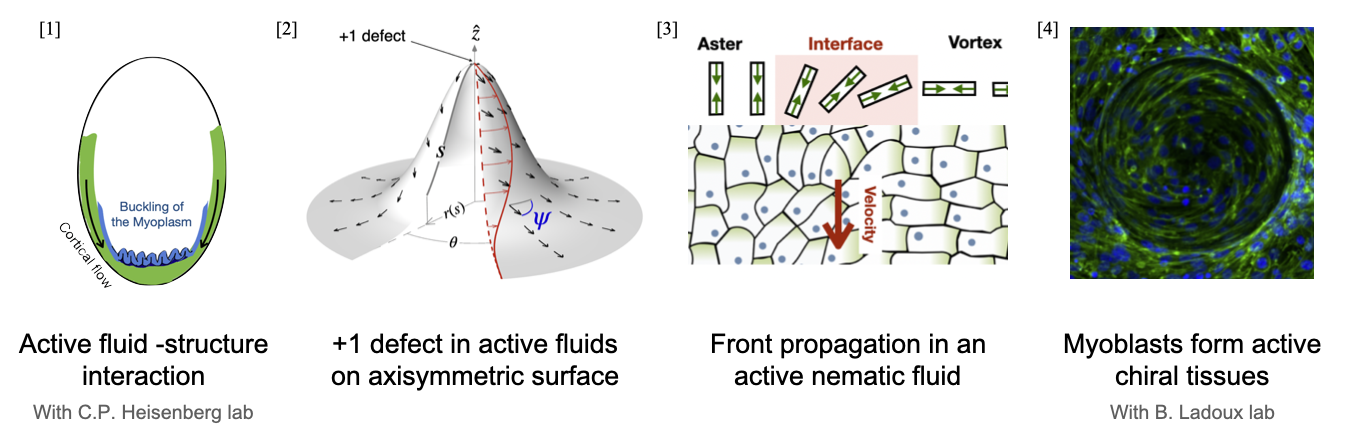
For example, shortly after fertilization of ascidian (also known as sea-squirts) embryo, actomyosin flows begin moving toward the opposite pole.
The myoplasm, a dense layer of mitochondria located just beneath the actomyosin-cortex, is influenced by this active flow.
As this cortical flow, flowing over the spherical myoplasm, progresses toward the other end of the egg, it causes the myoplasm to buckle. We show, using continuum theory of elastic sheets, how friction coupling between a passive surface and active flow is sufficient to explain the buckling phenomenon and subsequently its influence on cellular morphogenesis.
The public defense will take place on Monday, October 27, 2025, at 2:00 PM in the Pierre-Gilles De Gennes Amphitheater, Condorcet Building (Building A, underground). There will be a question-and-answer session afterwards, followed by a drinks reception in the common area on the 6th floor of the Condorcet Building. I know this falls during the university holiday week, so the campus will probably feel a bit quiet and not many people will be around. But if you happen to be around, feel free to join for the drinks — even if you don’t attend the defense itself : ).
Contact
Laboratoire Matière et Systèmes Complexes10 Rue Alice Domon et Léonie Duquet
75205 Paris Cedex 13
Email : irushikesh1996@gmail.com

In a nutshell
Epithelial tissues (thin layers of cells that cover our organs) or the actomyosin networks inside cells — Can be thought of as living materials. The actomyosin network is a molecular machine present inside cells, that allows cells to move and change shape by converting chemical energy (ATP) into mechanical work. When many such cells come together to form a tissue, these tiny molecular engines organize collectively, allowing the tissue itself to bend, flow, or change shape. Active hydrodynamics is a mathematical description that tries to capture the long-time fluid-like behavior of such a biological matter. A mathematical theory describing active fluids on curved surfaces had already been developed, since most biological tissues and cells naturally have curved shapes. In my thesis, I started from this existing theory and explored in detail how it behaves : In particular, how curvature affects the behavior of the active fluids. In addition to this theoretical work, we also collaborated with experimental biologists on two projects. In one, we studied how myoblast cells (the precursors of muscle cells) organize into chiral–helical structures on curved surfaces. In another, we examined how the actomyosin cortex — a thin active layer beneath the cell membrane — reorganizes right after fertilization in egg cells, and how this active fluid interacts with surrounding material to drive cell shape changes, thereby initiating embryogenesis.